
El coeficiente de Poisson es una cantidad adimensional, característica de cada material. Es un indicativo de la deformación de un trozo de material ante la aplicación de ciertos esfuerzos.
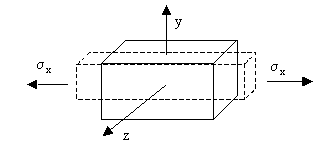
Cuando un trozo material que se somete a una tensión, o a una compresión, sufre una deformación, el cociente entre la deformación transversal y la deformación longitudinal es precisamente el coeficiente de Poisson.
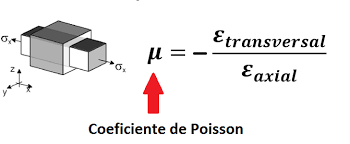
Fórmula del coeficiente de Poisson
Para calcular el coeficiente de Poisson es necesario determinar la deformación unitaria longitudinal y transversal.
La deformación unitaria longitudinal εL es el estiramiento dividido entre el largo original:
εL = (L’ – L) / L
De igual manera, la deformación unitaria transversal εT es el estrechamiento radial dividido entre el diámetro original:
εT = (D’ – D) / D
Por lo tanto, el coeficiente de Poisson se calcula mediante la siguiente fórmula:
ν = – εT / εL
Relación con el módulo de elasticidad y el módulo de rigidez
El coeficiente de Poisson ν, se relaciona con el módulo E de elasticidad (o módulo de Young) y con el módulo de rigidez G, mediante la siguiente fórmula:
ν = E /(2G) – 1
Relación de Poisson para algunos metales comunes:
| Metal | Coeficciente Poisson μ |
|---|---|
| Aluminio | 0,33 |
| Bronce de aluminio | 0,30 |
| Berilio | 0.024 - 0.03 |
| Hierro Fundido Corazón Negro | 0,26 |
| Bronce | 0,34 |
| Cobre | 0,36 |
| Oro | 0,42 |
| Dirigir | 0.40 - 0.45 |
| Magnesio | 0,35 |
| Acero suave | 0,3 |
| Molibdeno | 0,32 |
| Latón naval | 0,34 |
| Níquel | 0,31 |
| Bronce fosforado | 0,33 |
| Platino | 0,39 |
| Plutonio | 0.15 - 0.21 |
| Plata | 0,37 |
| Acero inoxidable 304L | 0,3 |
| Tantalio | 0,35 |
| Torio | 0.27 |
| Estaño | 0,33 |
| Titanio | 0,3 |
| Tungsteno | 0.28 |
| Uranio | 0,21 |
| Hierro forjado | 0,3 |
| Zinc | 0.25 |
