
Los engranajes planetarios es un conjunto de engranajes con el eje de entrada y el eje de salida alineados. Se utiliza una caja de engranajes planetarios para transferir el mayor par en la forma más compacta (conocida como densidad de par).

El centro de aceleración de la bicicleta es un gran ejemplo de un mecanismo de rueda planetaria: ¿Alguna vez se ha preguntado cómo puede obtener tanta potencia y capacidades en un centro tan pequeño? Para un cubo de tres velocidades, se utiliza un sistema de engranaje planetario de una etapa, para un cubo de cinco velocidades de 2 etapas. Cada sistema de engranaje planetario tiene un estado de reducción, un acoplamiento directo y un modo de aceleración.
En términos matemáticos, la relación de reducción más pequeña es 3: 1, la más grande es 10: 1. En una relación de menos de 3, el engranaje solar se vuelve demasiado grande contra los engranajes del planeta. En una proporción superior a 10, la rueda solar se vuelve demasiado pequeña y el par caerá. Las relaciones son generalmente absolutas, es decir, un número entero.
¿Dónde se utilizan los sistemas de engranajes planetarios?
Los engranajes planetarios a menudo se usan cuando el espacio y el peso son un problema, pero se necesita una gran cantidad de reducción de velocidad y torque. Este requisito se aplica a una variedad de industrias, incluidos tractores y equipos de construcción, donde se necesita una gran cantidad de torque para conducir las ruedas. Otros lugares donde encontrará juegos de engranajes planetarios incluyen motores de turbina, transmisiones automáticas e incluso destornilladores eléctricos.
Los sistemas de engranajes planetarios pueden producir una gran cantidad de torque porque la carga se comparte entre múltiples engranajes planetarios. Esta disposición también crea más superficies de contacto y un área de contacto más grande entre los engranajes que un sistema de engranaje de eje paralelo tradicional. Debido a esto, en la carga se distribuye de manera más uniforme y, por lo tanto, los engranajes son más resistentes al daño.
La forma más básica de engranaje planetario implica tres conjuntos de engranajes con diferentes grados de libertad. Los engranajes planetarios giran alrededor de los ejes que giran alrededor de un engranaje solar, que gira en su lugar. Una corona dentada une los planetas en el exterior y está completamente fija. La concentricidad del planeta que se agrupa con el sol y los engranajes anulares significa que el par se realiza a través de una línea recta. Muchos trenes de potencia son «cómodos» alineados en línea recta, y la ausencia de ejes compensados no solo disminuye el espacio, sino que elimina la necesidad de redirigir la potencia o reubicar otros componentes.
En una configuración planetaria simple, la potencia de entrada gira el engranaje solar a alta velocidad. Los planetas, espaciados alrededor del eje central de rotación, se engranan con el sol y con la corona dentada fija, por lo que se ven obligados a orbitar a medida que ruedan. Todos los planetas están montados en un solo miembro giratorio, llamado jaula, brazo o portador. A medida que el porta planetas gira, ofrece una salida de baja velocidad y alto par.
Relación entre los engranajes en un sistema de engranajes planetarios
Para determinar la relación entre el número de dientes del engranaje solar (za), los engranajes planetarios B (zb) y el engranaje interno C (zc) y el número de engranajes planetarios N en el sistema, estos parámetros deben satisfacer el siguientes tres condiciones:
Condición No.1
zc = za + 2 zb (17.1)
Esta es la condición necesaria para que las distancias centrales de los engranajes coincidan. Dado que la ecuación es verdadera solo para el sistema de engranajes estándar, es posible variar el número de dientes usando diseños de engranajes desplazados de perfil.
Para usar engranajes desplazados de perfil, es necesario hacer coincidir la distancia central entre el sol A y los engranajes del planeta B, a1, y la distancia central entre el planeta B y los engranajes internos C, α2.
α1 = α2 (17.2)
Condición No.2
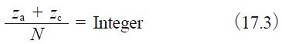
Esta es la condición necesaria para colocar engranajes planetarios espaciados uniformemente alrededor del engranaje solar. Si se desea una colocación desigual de engranajes planetarios, entonces se debe satisfacer la ecuación (17.4).
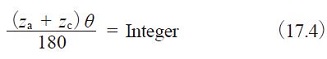
Donde θ : la mitad del ángulo entre engranajes planetarios adyacentes (°)
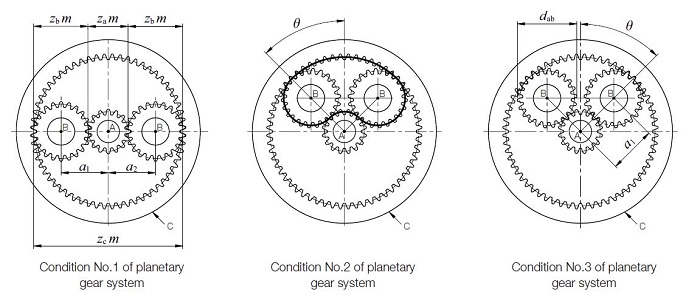
Condición No.3
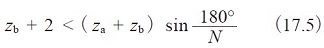

Satisfacer esta condición asegura que los engranajes planetarios adyacentes puedan operar sin interferir entre sí. Esta es la condición que debe cumplirse para un diseño de engranaje estándar con la misma colocación de engranajes planetarios. Para otras condiciones, el sistema debe satisfacer la relación:
Donde:
dab: Diámetro de la punta de los engranajes planetarios
α1: Distancia central entre el sol y los engranajes planetarios
Además de las tres condiciones básicas anteriores, puede haber un problema de interferencia entre el engranaje interno C y los engranajes del planeta B. Vea la Sección 4.2 Engranajes internos

Es muy interesante y practico podemos aprender y adquirir el conocimiento que requerimos
Saludos
Execelente me gustó
excelente artículo. didáctico e interesante. Felicitaciones